Hashing -Data Structure-Hashing in Java

 

Hashing

 

Why we need Hashing algorithm and how it differs from other algorithms

 

The main objective of Data Structure is effective way of organizing data in memory so that search and sort and other operations are fast.

Hashing is a special technique used to store and search data more effectively.

1.Compare with Array

We have 5 records and we want to store them in an effective way and retrieve any one from that collection. I want to search 13

 

Number iterations  5

Time Complexity O(n) ( n here denotes number of items in the Array)

 

 

 

 

 

2.Compare with Linked List

Trying search 13

 

Number of iterations 5

Time Complexity O(n)

 

3.Binary Search Tree

 

Number of iterations:4

Time complexity  O(log n)

/*For the input of size n, an algorithm of O(n) will perform steps proportional to n, while another algorithm of O(log(n)) will perform steps roughly log(n).

Clearly log(n) is smaller than n hence algorithm of complexity O(log(n)) is better. Since it will be much faster.

*/

Hash table a specialized array ,here we use special function called Hash function  to store and retrieve data in a collection.

But normal array we use index to store in a linear fashion.

 

Step 1: create a hash table

Step 2: Use a prime number

We have five records(5)

We need a prime number after the 5 that is 7

We need a hash function, it’s a mathematical formula .

A simple one is modulo operation

 

 

Search using Hash

We search 15

 

No of iterations 1  &Time Complexity O(1)

Collision:

Hash table size must be prime number, if we take the size as a non prime number:

Say for example the size is 8

 

While using prime number as size of Hashtable will also sometimes creates Collision.

To avoid that there are two methods:

 1.separate Chaining 2.Open Addressing

 

In separate chaining we use Linked List when collision occurs:

 Hash table size =7

 50%7=1  so 50 stored in 1^st index

700%7=0 so 700 goes to 0^th index

76%7=6 so 76 goes to 6^th index

85 %7

Search speed would be not o(1)

 

Open Addressing:

The main advantage is no linked is used here.A new technique will followed when collision occurs:

a)Linear probing

b)Quadratic Probing

c)Double Hashing

Linear probing is scheme in computer programming for resolving collisions in a hashtable data structures for maintaining a collection of key-value pairs and looking up a value associated with a given key.

 

Quadratic probing operates by taking the original hash index and adding successive values of an arbitrary  quadratic polynomial until  an open slot is found.

Double hashing a technique  used in conjunction with open addressing in hash tables to resolve hash collisions  by using a secondary hash of the key as an offset when a collision occurs

=============================================================

 

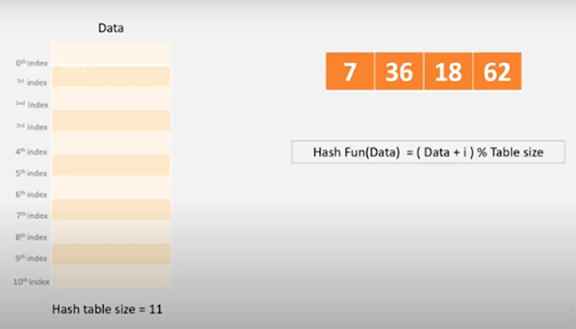
Linear probing

 

Initially i=0, if collision occurs value increased by 1, increasing the value linearly from 0 to 1,2.. and so on.

 

 Hash(7)=(7+0)%11=7

Hash(36)=(36+0)%11=3

Hash(18)=(18+0)%11=7(collision occurs)

Repeat Hash(18)=(18+1)%11=8

Hash(62)=(62+0)%11=11(collisoion)

Repeat hash(62)=(62+1)%11=8 collision

Repeat hash(62)=(62+2)%11=9

 

Quadratic Probing

Jumping will be done

 

 

Hash(7)=(7+0)%11=7

Hash(36)=(36+0)%11=3

Hash(18)=(18+0)%11=7 collision occurs

Hash(18)=(18+1)%11=8

Hash(62)=(62+0)%11=7 collision

Hash(62)=(62+1)%11=8 collision

Hash(62)=(62+(2*2))%11=0

 

 

 

Search

 

Time complexity in Hashing is o(1) If no collision comes.

If collision comes time complexity will be little bit more.